温度計を作る

表示はLCDで。

結論から言うと、、1KワードのROMでは、温度と電圧を同時にLCD表示させるのは難しそう。LCD制御で、かなり食ってしまいAD値から目的の値を算出するだけで終わってしまう。あ、そうか、足りなければ2個でやればいいんだな。

LM35

LM35でナショセミ（もうTIだけど）の温度センサーですよ。ちょっとした工作によく使いますよね。会社でも性格じゃない温度を測るのに使ってたりする。 PIC12F675で入門コースみたいなので、温度計みたいなのをLM35で作った事があるが、氷点下は測定できなかった。バイクに付けていつもの温度を測りたいと思っていて、許せばバッテリ電圧なども表示したら面白いかと。

LM35はナショセミの温度センサで、10mV/℃のリニア出力ができる。ナショセミは悲しい事に現在はTIに統合されてしまっている。

lm35.pdf

Calibrated directly in ° Celsius (Centigrade)
Linear + 10.0 mV/°C scale factor
0.5°C accuracy guaranteeable (at +25°C)
Rated for full -55° to +150°C range
Operates from 4 to 30 volts
Less than 60 µA current drain

精度もいいし、リニアリティ、計算も良いのだが、0℃以下が負電圧となってしまうと言うことがある。後で思う事だが、負電圧を作って且つ差動で増幅しても結局はLM60で計測するのと誤差と手間は同じだったように思う。

PICのADで読む

ADで読む方法では、分解能が4.8mVであるので、センサー出力を増幅しなければいけない。作成時は10倍にした。PIC12F675を使用したので内蔵ROMは1Kワードである。計算式は、Temp=AD*50／1024である。

unsigned int lm35_out,lm35_temp;
GO_DONE = 1;
while(GO_DONE);
lm35_out = (ADRESH<<8) | ADRESL ;
lm35_temp = lm35_out * 50/1024;

だけどこれだと、整数部分しか計算できない。10倍にして計算し、後で小数点の位置を変えようとすると、計算途中でlong型になってしまい、675だとちょっと厳しい。ソフト屋のT君にアドバイスをもらった。

(int)a = 498*5*10/1024                          //整数部の計算
(int)a =((498*5*10-1024a)*10)/1024      + (a*10)        //少数点の計算（10倍した値）と整数部（10倍した値）への足しこみ

う〜む、すばらし。

で、小数点2桁まで求めようとすると、どうなるんだろう。

LM60

あとでよくよく調べたら、LM61と言うのがあってこっちは、10mV/℃だった。

LM60は、6.25mV/℃のリニア出力で、424mVのオフセット付きである。なので、-25℃〜125℃が最大±3℃で測定できるとDataSheetに書いてある。この誤差は最大なので実際はもっと小さいと思われる。これをPICのADで直接読んで温度に変換したい。

電源5VでAD変換は最大10bitだから、5/1024=4.8mVちょっと。1℃以下の測定が無いに等しいから、アンプで増幅する事になるでしょう？オフセットが大きいので単純に10倍とかすると、測定範囲が狭くなってしまうじゃないですか。6倍ぐらいのゲインでギリギリだけど、10倍ぐらいにしてオフセット切ってやれば表示精度が上げられそうじゃない？
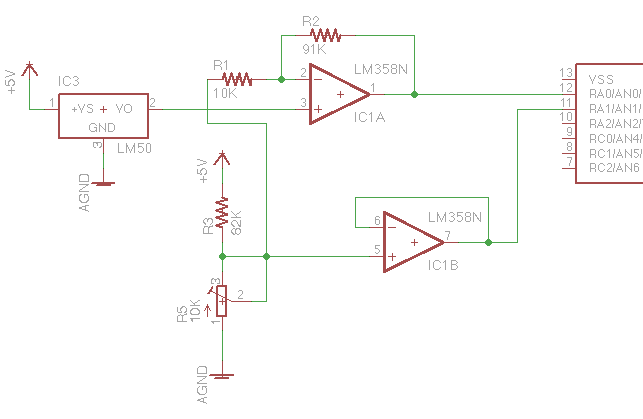
で、回路。使っているICとか部品名が違うけど気にしないで（Eagleのライブラリに無かったから適当）

オフセットを固定で切ってやると、後で調整するときに面倒だしそれに、電源電圧がいつも5Vと限らないでしょう。なので、ADを二つ使って誤差を埋めてやれば、演算だけで出来そうじゃ無いですか？。回路図のLM358はLM2904を使用、GND側は入出力ともRail動作。

計算

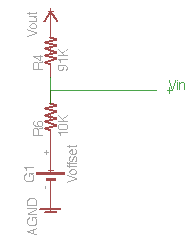
上の回路だと、非反転増幅のGND部分にオフセッットが入るから、-,+入力が仮想短絡になるよう制御されるので、Vinをセンサ出力だとすると次のようになると思う。

Vin＝（Vout-Voffset)x10/(91+10)+Voffset
よって、Vout＝(Vin-Voffset)x101/10+Voffset　となる。なんで、このような面倒な計算なの？って、そりゃ、間違えて回路作っちゃたからでしょ。ちょっと勘違いして配線して、結果を見たら違うって言うよくある話で。

以下の計算式は、差動増幅で、オフセットのみ捕れた場合の算出方法で、結論から言うと、今回の計算は下記になるですな。

Temp＝（1/1.280）×（（AD1-AD2）/10.1+AD2）ー67.84

まず前提

センサAmpの倍率＝10.1。ぴったりの抵抗が無いのよ、面倒。
オフセット調整範囲＝0.543V〜0V　実際にはもっと範囲狭くなる。
センサ電圧＝V_Temp。
AN0入力　AD変換値をAD1とし、AD1の電圧＝V_AD1
AN1入力　AD変換値をAD2とし、AD2の電圧＝V_AD2
使用範囲を-20℃以上と考えると、0.3Vオフセット出せれば良い。
オフセット側のアンプは、AD入力インピーダンスがキット低いから。

んで、以下の式になる。

（V_TempーV_AD2）×10.1＝V_AD1　となり、変形すると、
V_Temp＝V_AD1／10.1＋V_AD2

となる。一方、実温度は、0℃＝424mVであることと、ΔT=6.25mV/℃の関係から

T＝（V_Tempー0.424）／6.25×10^-3

である。

また、AD値と電圧の関係は、

V_AD1＝AD1×5／1024

V_AD2＝AD2×5／1024

よって最初の式から

V_Temp＝（AD1×5／1024）／10.1＋AD2×5／1024

2番めの式と、上式から温度は

Temp＝（1/1024）×（AD1×5/10.1＋AD2×5）−0.424 }／6.25×10^-3

数字同士の部分を計算すると、下式になる。

Temp＝（1/1.280）×（AD1/10.1+AD2）ー67.84

上式の最後の項は定数である（AD値に左右されない）。
ここで、大きな問題がある。これは実数計算であり、double型でこの計算すると、LCDも表示制御があるので、2Kワードでは無理である。困った。

演算

Temp＝（1/1.280）×（AD1/10.1+AD2）ー67.84

このままだど、double演算になるので、整数に直さないといけない。そこで分母分子で同倍する。AD値を100倍にして、分母も100倍。すると、下記

Temp＝（AD1×100/10＋AD2×100）／1280＋67

最後の67は、67.84を切り捨てで算出。整数演算は切り捨てになるからというのと、エクセルで計算させると切り捨てのの方が真値に近かった。アンプゲイン10.1は、10倍でも誤差は変わらなかった。

結論

いきなり、結論。この方法はよろしくない。

オフセットをとる電圧が誤差を含み、そのまま増幅されてしまうのでものすごく誤差が出る。う〜ん、誤差と言うかバラツキ？値がコロコロ変わる。だいたい合っているとき合ってない時がある。

というわけで、計算しやすいLM61に変更し作り直した。→　温度計を作る2

目次

温度計を作る

LM35

PICのADで読む

LM60

計算

演算

結論